Đề thi Tuyển sinh lớp 10 chuyên Tin tỉnh Quảng Ninh 2025
[Quảng Ninh - TS10 - 2025] Bài 1: Ước số
Nộp bàiPoint: 30
Số nguyên dương ~a~ được gọi là ước nguyên dương thực sự của số nguyên ~n~ nếu ~a~ là ước của ~n~ và ~a < n~. Ví dụ số ~24~ có ~7~ ước nguyên dương thực sự là: ~1, 2, 3, 4, 6, 8, 12~.
Yêu cầu: Hãy xác định ước nguyên dương thực sự lớn nhất của ~n~.
INPUT
Gồm một dòng chứa số nguyên dương ~n~ (~2 \le n \le 10^5~).
OUTPUT
Ước nguyên dương thực sự lớn nhất của ~n~.
SAMPLE INPUT 1
4
SAMPLE OUTPUT 1
2
SAMPLE INPUT 2
7
SAMPLE OUTPUT 2
1
SAMPLE INPUT 3
24
SAMPLE OUTPUT 3
12
[Quảng Ninh - TS10 - 2025] Bài 2: Tổng dãy
Nộp bàiPoint: 30
Cho một dãy gồm ~n~ số nguyên dương ~a_1, a_2, ..., a_n~.
Yêu cầu: Đếm số cặp ~(i, j)~ đồng thời thỏa mãn:
- ~1 \le i < j \le n;~
- ~a_i + a_{i+1} + ... + a_j~ là một số chẵn.
INPUT
Dòng đầu chứa số nguyên dương ~n~ (~2 \le n \le 10^5~);
Dòng thứ hai chứa ~n~ số nguyên dương ~a_1, a_2, ..., a_n~ (~1 \le a_i \le 10^9; i = 1, 2, ..., n~).
OUTPUT
Số lượng cặp ~(i, j)~ thỏa mãn yêu cầu của bài.
SAMPLE INPUT 1
5
1 2 3 4 5
SAMPLE OUTPUT 1
4
Giải thích: Số cặp thỏa mãn là (~1, 3~), (~1, 4~), (~2, 5~), (~3, 5~).
SAMPLE INPUT 2
4
2 5 6 4
SAMPLE OUTPUT 2
1
SUBTASKS
| Subtask | Điểm | Ràng buộc |
|---|---|---|
| 1 | ~40\%~ | ~n \le 10^2~. |
| 2 | ~40\%~ | ~10^2 < n \le 5 \times 10^3~. |
| 3 | ~20\%~ | Không có ràng buộc gì thêm. |
[Quảng Ninh - TS10 - 2025] Bài 3: Trung vị
Nộp bàiPoint: 25
Dãy ~A~ gồm ~n~ số nguyên ~a_1, a_2, ..., a_n~ được gọi là dãy không giảm nếu thỏa mãn: ~a_1 \le a_2 \le ... \le a_n~.
Trung vị của dãy các số nguyên ~a_1, a_2, ..., a_n~ là phần tử xuất hiện ở vị trí ~[\frac{n+1}{2}]~ sau khi dãy đó được sắp xếp lại thành dãy không giảm.
Ví dụ: Cho dãy ~A = (2, 3, 4, 2, 8)~ sau khi sắp xếp lại thành dãy không giảm ta được dãy ~(2, 2, 3, 4, 8)~, trung vị của dãy là phần tử ~3~; dãy ~B = (3, 5, 7, 6)~ sau khi sắp xếp lại thành dãy không giảm ta được dãy ~(3, 5, 6, 7)~, trung vị của dãy là phần tử ~5~. Trung vị của dãy chỉ có một phần tử là chính phần tử đó.
Yêu cầu: Cho dãy ~A~ gồm ~n~ số nguyên ~a_1, a_2, ..., a_n~ và số nguyên ~k~. Hãy xác định trung vị lớn nhất của mọi dãy con gồm ít nhất ~k~ phần tử liên tiếp trong dãy đã cho.
INPUT
Dòng đầu chứa hai số nguyên ~n, k~ (~1 \le k \le n \le 10^5~);
Dòng thứ hai chứa ~n~ số nguyên ~a_1, a_2, ..., a_n~ (~1 \le a_i \le n; i = 1, 2, ..., n~).
OUTPUT
In ra kết quả bài toán.
SAMPLE INPUT 1
4 2
1 3 2 4
SAMPLE OUTPUT 1
3
Giải thích:
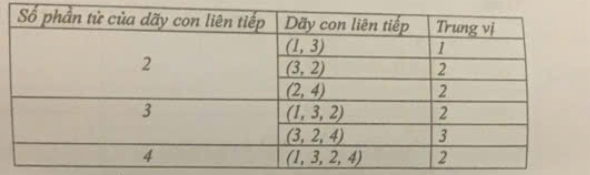
SAMPLE INPUT 2
4 1
1 2 2 4
SAMPLE OUTPUT 2
4
SAMPLE INPUT 3
11 2
3 2 3 2 11 5 2 3 9 10 11
SAMPLE OUTPUT 3
10
SAMPLE INPUT 4
11 6
3 2 3 2 11 5 2 3 9 10 11
SAMPLE OUTPUT 4
9
SUBTASKS
| Subtask | Điểm | Ràng buộc |
|---|---|---|
| 1 | ~20\%~ | ~k = 2, n = 3~. |
| 2 | ~20\%~ | ~k = 1~ |
| 3 | ~30\%~ | ~n \le 100~ |
| 4 | ~30\%~ | Không có ràng buộc gì thêm. |
[Quảng Ninh - TS10 - 2025] Bài 4: Dãy con tăng
Nộp bàiPoint: 15
Cho dãy ~a~ gồm ~n~ số nguyên ~a_1, a_2, ..., a_n~.
Giá trị ~n~ được gọi là độ dài của dãy ~a~.
Dãy con của ~a~ là chính ~a~ hoặc là dãy nhận được từ dãy ban đầu bằng cách bỏ đi một số phần tử.
Dãy ~a~ được gọi là dãy không giảm nếu thỏa mãn: ~a_1 \le a_2 \le ... \le a_n~.
Ví dụ dãy: ~[2, 2, 4, 9, 3, 10]~ ta có một số dãy con như sau: ~[2, 2, 4, 10]~; ~[2, 9]~; ~[3, 2, 9, 10]~.
Trong đó, các dãy con ~[2, 2, 4, 10]~ và ~[2, 9, 10]~ được gọi là các dãy con không giảm.
Cho dãy ~a~ gồm ~n~ số nguyên, dãy ~b~ gồm ~m~ số nguyên. Dãy ~c~ được gọi là dãy con chung của hai dãy ~a~ và ~b~ nếu ~c~ vừa là dãy con của ~a~, vừa là dãy con của ~b~.
Ví dụ: Cho dãy ~a = (1, 2, 4, 9, 3)~ và dãy ~b = (0, 2, 15, 9)~. Dãy ~c = (2, 9)~ là một dãy con chung của hai dãy ~a~ và ~b~.
Yêu cầu: Cho hai dãy ~a~ và ~b~ chỉ chứa các số ~0~ và ~1~, dãy ~a~ có ~n~ phần tử, dãy ~b~ có ~m~ phần tử. Hãy xác định độ dài lớn nhất của dãy con chung không giảm của ~a~ và ~b~.
INPUT
Dòng đầu tiên chứa số nguyên dương ~n~ (~1 \le n \le 2 \times 10^5~) là số phần tử của dãy ~a~.
Dòng thứ hai chứa ~n~ số nguyên dương ~a_1, a_2, ..., a_n~ (~0 \le a_i \le 1~) là các phần tử của dãy ~a~.
Dòng thứ ba chứa số nguyên dương ~m~ (~1 \le m \le 2 \times 10^5~) là số phần tử của dãy ~b~.
Dòng thứ tư chứa ~m~ số nguyên dương ~b_1, b_2, ..., b_m~ (~0 \le b_i \le 1~) là các phần tử của dãy ~b~.
Dữ liệu đảm bảo luôn tồn tại dãy con chung.
OUTPUT
Độ dài lớn nhất của dãy con chung không giảm của hai dãy ~a~ và ~b~.
SAMPLE INPUT 1
7
0 0 0 1 0 1 1
6
0 0 1 1 0 1
SAMPLE OUTPUT 1
5
Dãy con chung không giảm dài nhất là ~0, 0, 1, 1, 1~.
SAMPLE INPUT 2
10
0 0 0 1 1 1 0 1 0 0
10
1 1 0 0 0 1 0 1 1 1
SAMPLE OUTPUT 2
7
SAMPLE INPUT 3
3
1 1 1
5
1 0 1 0 0
SAMPLE OUTPUT 3
2
SUBTASKS
| Subtask | Điểm | Ràng buộc |
|---|---|---|
| 1 | ~25~ | ~a_i = 1~, ~m, n \le 3000~. |
| 2 | ~25~ | ~m = n~, ~a_i = b_i~ |
| 3 | ~25~ | ~m, n \le 3000~ |
| 4 | ~25~ | Không có ràng buộc gì thêm. |